Calculate Your Chances of Playing as Impostor in Among Us
A Polish student has created a digital calculator that makes it easy to see the percentage chance of playing as the impostor in Among Us.
It certainly happened to you during a game in Among Us that you felt frustration with the fact that you didn't draw the role of impostor for several rounds in a row. The many options we get from being the killer, as well as the excitement that accompanies it, make the average player simply prefer sowing fear on the spaceship to completing menial tasks.
Enter Maciej Kowalski, a Polish student of mathematics and cognitive science, decided to clear our doubts and create a calculator which, after entering the relevant data (such as the number of games, participants in the game and impostors in each game), will create a clear chart and give us a percentage chance to be chosen as the impostor. All of this is part of a special website and also a startup initiative called Omni Calculator, which enables us to calculate many different (more or less strange) values, including, for example, those related to sunbathing or studying the magnitude of an earthquake.
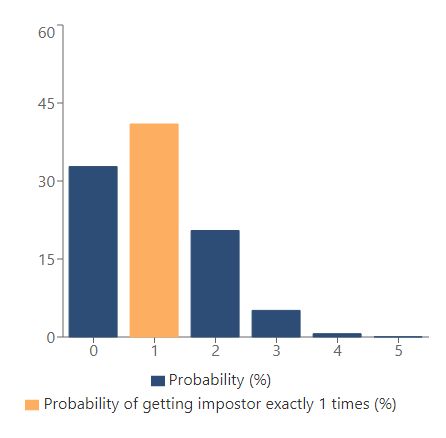
Since we all know how this digital device works, it's also worth seeing what that about chances of being an impostor. We did a simple test that included the following parameters - 5 games, two impostors in each of them, and a total of 10 participants. From this, we calculate the percentage probability of being chosen as the impostor at least once. It is exactly 41%, so not a low value at all. And here's the graph generated by Omni Calculator:
We learned about this feature thanks to Inverse. It was also on its pages that Maciej Kowalski talked about the idea for this particular calculator. It was said to have taken place one day, when the developer of the system, together with his friends, took part in a tournament in Among Us. It was then that he was supposed to draw the role of the impostor so many times that curiosity did not allow him to leave the case without a precise diagnosis. People familiar with the subject will probably be interested in the fact that the study used a probability distribution called a binomial distribution.
